Question

An unknown element is a mixture of isotopes ¹²⁰X and ¹²²X. The average atomic mass of X is 120.59 amu. What is the percent abundance of ¹²²X?

Answer 1

`\%_(X-122)=29.5\%`

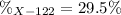
Step-by-step explanation:

Hello!

In this case, since isotopes are atoms of the same element with equal number of protons and electrons but different atomic mass, we can write the equation used to compute the average atomic mass of the considered X:

`m_X^(avr)=\%_(X-120)*120+\%_(X-122)*122`

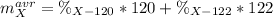
However since both percentages compose the 100%, we can write one of those in terms of the other:

`m_X^(avr) = (100\%-\%_(X-122))*120+\%_(X-122)*122`

Thus, we can solve for the percent abundance of X-122 as shown below:

`120.59 = 120-\%_(X-122)*120+\%_(X-122)*122\\\\120.59-120=\%_(X-122)(122-1200)\\\\120.59-120=\%_(X-122)*2\\\\\%_(X-122)=(0.59)/(2)=29.5\%\\`

Thus the percent abundance of the other isotope would be 70.5 %.

Best regards!