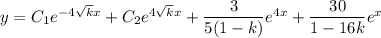Question

D^2(y)/(dx^2)-16*k*y=9.6e^(4x) + 30e^x

Answer 1

The solution depends on the value of
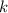
`k`. To make things simple, assume
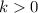
`k>0`. The homogeneous part of the equation is


`(\mathrm d^2y)/(\mathrm dx^2)-16ky=0`

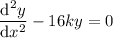
and has characteristic equation


`r^2-16k=0\implies r=\pm4\sqrt k`

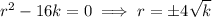
which admits the characteristic solution
`y_c=C_1e^(-4\sqrt kx)+C_2e^(4\sqrt kx)`.

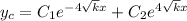
For the solution to the nonhomogeneous equation, a reasonable guess for the particular solution might be
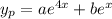
`y_p=ae^(4x)+be^x`. Then


`(\mathrm d^2y_p)/(\mathrm dx^2)=16ae^(4x)+be^x`

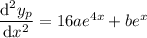
So you have


`16ae^(4x)+be^x-16k(ae^(4x)+be^x)=9.6e^(4x)+30e^x`

`(16a-16ka)e^(4x)+(b-16kb)e^x=9.6e^(4x)+30e^x`

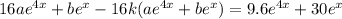
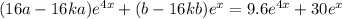
This means


`16a(1-k)=9.6\implies a=\frac3{5(1-k)}`

`b(1-16k)=30\implies b=(30)/(1-16k)`

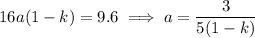
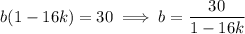
and so the general solution would be


`y=C_1e^(-4\sqrt kx)+C_2e^(4\sqrt kx)+\frac3{5(1-k)}e^(4x)+(30)/(1-16k)e^x`