Question

The drama club was selling ticketsto the school play. Adult ticketscost $8.00 each, and studenttickets cost $5.00 each. The littletheater holds 142 people and wassold out for both Friday andSaturday. The total sales for thetwo days was $1,948.00.1. How many adult tickets weresold out over the two days?2. How many student tickets weresold out over the two days?

Answer 1

We are given a problem that can be solved using a system of linear equations. Let A, be the number of adults, and S the number of students. Since there are in total 142 people and there were two days, this means that the sum of the number of adults and the number of students must be 284, which can be written mathematically as follows:

`A+S=284,(1)`

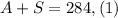
This is our first equation. The second equation is found using the total sales of $1948. Since the ticket per adult is $8 and per student is $5, we have the following equations:

`8A+5S=1948,(2)`

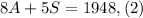
To solve this equation we will solve for A in equation (1), by subtracting S to both sides;

`\begin{gathered} A+S-S=284-S \\ A=284-S \end{gathered}`

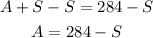
Now we will replace this value in equation (2):

`8(284-S)+5S=1948`

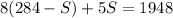
Now we will apply the distributive property:

`2272-8S+5S=1948`

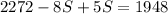
Addins like terms:

`2272-3S=1948`

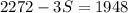
Subtracting 2272 to both sides;

`\begin{gathered} 2272-2272-3S=1948-2272 \\ -3S=-324 \end{gathered}`

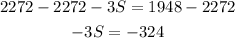
Dividing both sides by -3:

`S=-(324)/(-3)=108`

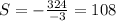
Now we replace this value in equation (1), where we have already solved for A:

`\begin{gathered} A=248-108 \\ A=140 \end{gathered}`

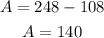
Therefore, there were sold 108 student tickets and 140 adult tickets.