ANSWER
y = -x - 3
STEP BY STEP EXPLANATION
Step 1: The given points are:
(-6, 3) and (5, -8)
Step 2: The slope-intercept form is
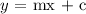
where m is the slope and c is the intercept
Step 3: Find the slope m
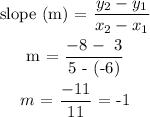
Step 4: Solve for intercept c using either of the points
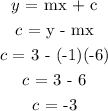
Step 5: Re-writing the slope-intercept form to include the values of m and c
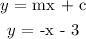
Hence, the equation of the line in slope-intercept form is y = -x - 3