Answer:
The area of the DVD is
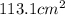 (rounded to the nearest hundredth).
(rounded to the nearest hundredth).
Explanation:
The figure below is a circle of diameter 12 centimeter in the Cartesian coordinate system.
The area of a circle is
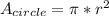 [ 1 ].
[ 1 ].
We know that
 , where d is the diameter (or the line segment that passes through the center of a circle and whose endpoints lie on it) and r is the radius of the circle (the distance from the circle's center to the circle's circumference).
, where d is the diameter (or the line segment that passes through the center of a circle and whose endpoints lie on it) and r is the radius of the circle (the distance from the circle's center to the circle's circumference).
Similarly, the circumference of a circle is the distance around a circle (the red line in the figure below).
The constant
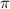 is a Greek symbol and is determined by dividing the circumference of a circle by its diameter:
is a Greek symbol and is determined by dividing the circumference of a circle by its diameter:
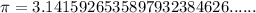 , although in practice
, although in practice
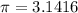 .
.
To find what the DVD area is, and considering it as a circle, we can determine the area using [ 1 ].
We also know that
 , or:
, or:
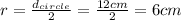 .
.
So, the area of the DVD, with diameter of 12 centimeters is:
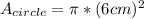
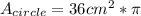 or
or
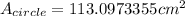 or rounded to the nearest hundredth:
or rounded to the nearest hundredth:
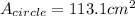 (Because 0.097 =
(Because 0.097 =
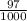 ≈
≈
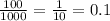 ).
).
So, the a DVD with diameter of 12 centimeters has an area of
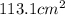 (rounded to the nearest hundredth).
(rounded to the nearest hundredth).