Answer:
Option D
Explanation:
Given that the number of hours of daylight in a city in the northern hemisphere shows periodic behavior over time
Let t be the independent variable and no of hours H(t) be the dependent variable on t.
Maximum H(t) = 14.4 and average =12
Period = 365 days
If we fix a sine curve for this since period is 365, we must have coefficient of t as
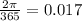
So the function H(t) will have sine term as sin 0.017t ... i
Since average = 12, we have
H(t) = 12+a sin 0.017t
for some suitable a.
To find a, use maximum
Maximum is when angle is 90 degrees i.e. when sine value =1
max H(5) = 14.4 = 12+a (1)
a =2.4
Hence correct equation would be'H(t) = 2.4sin(0.017t)+12
OPtion D is right answer.