Answer: The equation of the line in slope-intercept form is y = x.
Step-by-step explanation: We are given to find the equation in slope-intercept form of the line that is perpendicular to the line y - 4 = -(x - 6) and passes through the points (-2, -2).
PERPENDICULAR LINES: The product of the slopes of two perpendicular lines is -1.
The slope-intercept form of the given line is
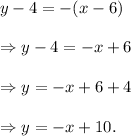
So, slope of the line, m = co-efficient of x = 1.
Let 'n' be the slope of the perpendicular line, so we have

Therefore, the slope-intercept form of the line with slope n = 1 and passing through the point (-2, -2) will be

Thus, the slope-intercept form of the line is y = x.