Answer: C)
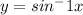
Explanation:
Since, the graph of an inverse trigonometric function will pass through the point
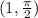 ,
,
If this point satisfies the function,
For the function
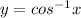
If x = 1
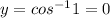
Thus,
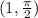 is not satisfying function
is not satisfying function
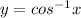 ,
,
⇒ The graph of
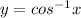 is not passing through the point
is not passing through the point
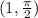
For the function
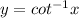
If x = 1
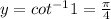
Thus,
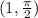 is not satisfying function
is not satisfying function
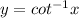 ,
,
⇒ The graph of
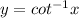 is not passing through the point
is not passing through the point
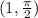
For the function
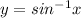
If x = 1

Thus,
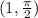 is satisfying function
is satisfying function
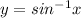 ,
,
⇒ The graph of
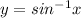 is passing through the point
is passing through the point
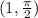 .
.
For the function
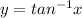
If x = 1

Thus,
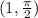 is not satisfying function
is not satisfying function
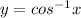 ,
,
⇒ The graph of
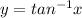 is not passing through the point
is not passing through the point
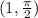 .
.
Hence, Option C is correct.