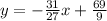Question

Please help me work through this homework problem! thank you!

Answer 1

Given:

Given the function

`y=3+(3)/(x)+(2)/(x^2)`

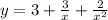
and a point x = 3.

Required: Equation of the line tangent to y at x = 3.

Step-by-step explanation:

The derivative of a function is he slope of the tangent line of the function at a given point. So, finding the derivative gives the slope of the tangent line.

`y^(\prime)=-(3)/(x^2)-(4)/(x^3)`

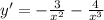
Substitute 3 for x into the derivative.

`\begin{gathered} y^(\prime)|_(x=3)=-(3)/(3^2)-(4)/(3^3) \\ =-(31)/(27) \end{gathered}`

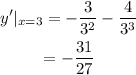
Therefore, the slope of the tangent line is -31/27.

Substitute 3 for x into y.

`\begin{gathered} y|_(x=3)=3+(3)/(3)+(2)/(3^2) \\ =3+1+(2)/(9) \\ =4+(2)/(9) \\ =(38)/(9) \end{gathered}`

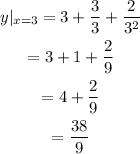
(3, 38/9) is the only point on the tangent line where it intersects the original graph.

Plug these coordinates along with slope into the general point-slope form to find the equation.

`\begin{gathered} y-y_1=m(x-x_1) \\ y-(38)/(9)=-(31)/(27)(x-3) \end{gathered}`

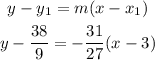
Solving for y will give the equation in slope-intercept form.

`\begin{gathered} y=-(31)/(27)(x-3)+(38)/(9) \\ =-(31)/(27)x+(69)/(9) \end{gathered}`

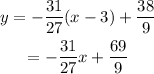
Final Answer: The equation of the tangent line is

`y=-(31)/(27)x+(69)/(9)`