Answer:

Explanation:
The average rate of change of the function between
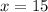 and
and
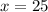 is given by the formula;
is given by the formula;
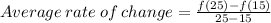
From the table,
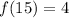 .
.
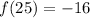 .
.
We substitute the values to obtain;
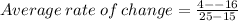
This will give us,

We now simplify to obtain,
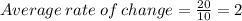
Therefore the average rate of change of the function from
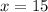 to
to
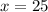 is
is
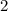 degrees celsius.
degrees celsius.