Question

The length of a rectangle is 3 inches greater than the width. (Hint: draw a pictureand label itA. Write a polynomial that represents the area of the rectangle.B. Find the area of the rectangle when the width is 4 inches..

Answer 1

We are given that the length of a rectangle is 3 inches greater than the width.

Let us draw a rectangle and label the width and length.

Part A:

Let the width of the rectangle is x inches.

Then the length of the rectangle is (x + 3) inches.

Now recall that the area of a rectangle is given by

`A=L\cdot W`

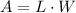
Where L is the length and W is the width of the rectangle.

`\begin{gathered} A=(x+3)\cdot x \\ A=x^2+3x \end{gathered}`

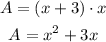
Therefore, the above polynomial represents the area of the rectangle.

Part B:

We are given that the width is 4 inches.

Substitute the width (x = 4) into the equation of the area that we found in part A.

`\begin{gathered} A=x^2+3x \\ A=(4)^2+3(4) \\ A=16+12 \\ A=28in^2 \end{gathered}`

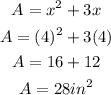
Therefore, the area of the rectangle is 28 square inches.