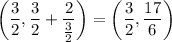Question

Examine the function

f(x) = x + (2/x)
Find the point on the curve at which the tangent lines pass through the point (3, 3).
(x,y) = ?

Answer 1

The tangent line to the function's graph at any point
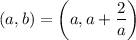
`(a,b)=\left(a,a+\frac2a\right)` has slope


`f'(x)=1-\frac2{x^2}`

and thus has the equation


`y-a-\frac2a=\left(1-\frac2{a^2}\right)(x-a)\implies y=\left(1-\frac2{a^2}\right)x+\frac4a`

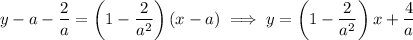
Any such line that passes through (3,3) will then satisfy


`3=\left(1-\frac2{a^2}\right)3+\frac4a\mplies\frac6{a^2}=\frac4a`


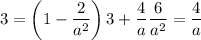
`a` clearly can't be 0, so we can divide both sides by
`\frac1a` to end up with


`\frac6a=4\implies a=\frac64=\frac32`

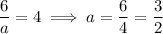
So the only point that answers the question is
`\left(\frac32,\frac32+\frac2{\frac32}\right)=\left(\frac32,\frac{17}6\right)`