Question

Can you explain what the 8th question is asking then answer it please

Answer 1

Options A and C

Explanation:

We want to find out which arithmetic sequence(s) contain the term 34.

For an arithmetic sequence to contain the term, 34, the corresponding n-value must be an integer.

Option A

Set tn = 34

`\begin{gathered} t_n=6+(n-1)4 \\ 34=6+(n-1)4 \end{gathered}`

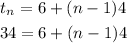
Solve for n:

`\begin{gathered} 34-6=4n-4 \\ 28=4(n-1) \\ n-1=(28)/(4)=7 \\ n-1=7 \\ n=7+1 \\ n=8 \end{gathered}`

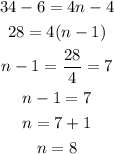
The 8th term of this sequence is 34.

Option B

`\begin{gathered} t_n=3n-1 \\ 34=3n-1 \\ 34+1=3n \\ 35=3n \\ n=(35)/(3)=11(2)/(3) \end{gathered}`

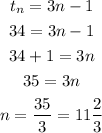
A sequence cannot have a decimal nth term, therefore, the sequence does not contain 34.

Option C

T1 = 12, d=5.5

`\begin{gathered} 12+5.5(n-1)=34 \\ 5.5(n-1)=34-12 \\ 5.5(n-1)=22 \\ n-1=(22)/(5.5) \\ n=4+1 \\ n=5 \end{gathered}`

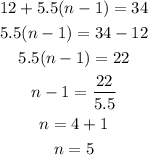
The 5th term of this sequence is 34, therefore, it contains the term 34.

Option D

3,7,11,...

`\begin{gathered} t_1=3 \\ d=7-3=4 \end{gathered}`

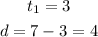
Using the nth term of an arithmetic sequence formula:

`\begin{gathered} t_n=t_1+(n-1)d \\ 34=3+4(n-1) \\ 34-3=4(n-1) \\ 31=4(n-1) \\ n-1=(31)/(4) \\ n-1=7(3)/(4) \\ n=8(3)/(4) \end{gathered}`

A sequence cannot have a decimal nth term, therefore, the sequence does not contain 34.

The sequences in Options A and C contain the term 34.