By the polynomial remainder theorem, the remainder upon dividing
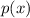
by
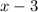
will be the value of
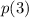
.
... | 1 ... -6 ... -4 ... -6 .... -2
3. | .. ... 3 ... -9 ... -39 .. -135
--------------------------------------
... | 1 ... -3 ... -13 . -45 .. -137
So you have
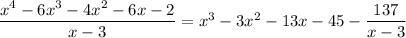
which means
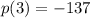
.