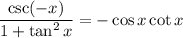Answer:
The simplified expression is:
Option: c
c. -cos(x)cot(x)
Explanation:
We are asked to simplify the expression:
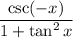
We know that :
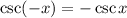
Also, we know that:
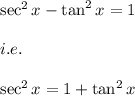
i.e.
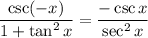
Also, we know that:
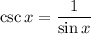
and
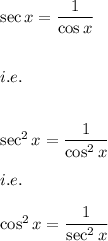
Hence, we have:
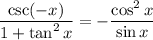
which could also be written as:
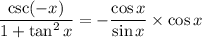
Now, we have:
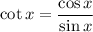
Hence, we get: