• Given the dimensions of ABCD:
m∠A = 71.68 degrees
m∠C = 47.68 degrees
m∠D = 141.87 degrees
CD = 4
AD = 6
BC = 8
• Dimensions of KLMN:
m∠K = 71.52 degrees
m∠L = 98.87 degrees
m∠M = 47.53 degrees
KL = 10
KN = 15
MN = 10
Let's find the missing values.
Given that figure ABCD is a dilation of KLMN, both figures are similar.
• Similar figures have proportional corresponding sides.
,
• Similar figures have equal corresponding angles.
Therefore, we have the corresponding sides:
AB ⇔ KL
BC ⇔ LM
CD ⇔ MN
AD ⇔ KN
The corresponding angles are:
m∠A = m∠K
m∠B = m∠L
m∠C = m∠M
m∠D = m∠N
Thus, to find the missing values, we have:
• X = m∠B = m∠L = 98.87 degrees
X = 98.87 degrees.
• Y = m∠N = m∠D = 141.87 degrees.
Y = 141.87 degrees
• To find the value of ,a,, apply the proportionality equation:
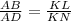
Plug in values and solve for a:

• To find the value of ,b,, apply the proportionality equation:
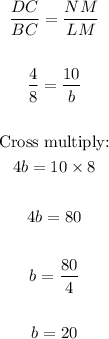
ANSWER:
• X = 98.87°
,
• Y = 141.87°
,
• a = 4
,
• b = 20