Question

Given that figure ABCD is a dilation of figure KLMN, find the missing values:(note that values are slightly different because of a round-off error)

Answer 1

• Given the dimensions of ABCD:

m∠A = 71.68 degrees

m∠C = 47.68 degrees

m∠D = 141.87 degrees

CD = 4

AD = 6

BC = 8

• Dimensions of KLMN:

m∠K = 71.52 degrees

m∠L = 98.87 degrees

m∠M = 47.53 degrees

KL = 10

KN = 15

MN = 10

Let's find the missing values.

Given that figure ABCD is a dilation of KLMN, both figures are similar.

• Similar figures have proportional corresponding sides.

,

• Similar figures have equal corresponding angles.

Therefore, we have the corresponding sides:

AB ⇔ KL

BC ⇔ LM

CD ⇔ MN

AD ⇔ KN

The corresponding angles are:

m∠A = m∠K

m∠B = m∠L

m∠C = m∠M

m∠D = m∠N

Thus, to find the missing values, we have:

• X = m∠B = m∠L = 98.87 degrees

X = 98.87 degrees.

• Y = m∠N = m∠D = 141.87 degrees.

Y = 141.87 degrees

• To find the value of ,a,, apply the proportionality equation:

`(AB)/(AD)=(KL)/(KN)`

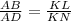
Plug in values and solve for a:

`\begin{gathered} (a)/(6)=(10)/(15) \\ \\ \text{Cross multiply:} \\ 15a=10*6 \\ \\ 15a=60 \\ \\ a=(60)/(15) \\ \\ a=4 \end{gathered}`

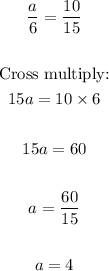
• To find the value of ,b,, apply the proportionality equation:

`\begin{gathered} (DC)/(BC)=(NM)/(LM) \\ \\ (4)/(8)=(10)/(b) \\ \\ \text{Cross multiply:} \\ 4b=10*8 \\ \\ 4b=80 \\ \\ b=(80)/(4) \\ \\ b=20 \end{gathered}`

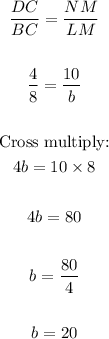
ANSWER:

• X = 98.87°

,

• Y = 141.87°

,

• a = 4

,

• b = 20