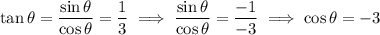If

is the variable of the horizontal axis, then you can solve for
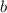
to get the equation of the line in slope-intercept form in the
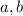
plane:
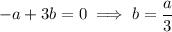
i.e. a line with slope

through the origin, which means it is contained in the first and third quadrants. Since the terminal side of
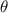
has a negative sine, the angle must lie in the third quadrant.
Because the slope of the line is

, you can choose any length along the line to make up the hypotenuse of a right triangle with reference angle
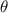
. Any such right triangle will have
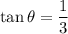
, regardless of whether the angle is the first or third quadrant. But since
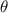
is known to lie in the third quadrant, and so
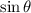
and
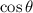
are both negative, you have