Question

Before you is a pile of 8 blocks: 4 are white, 3 are yellow, and 1 is purple. By placing the blocks side by side in a straight line, how many different color patterns could you make?

A.
288

B.
140

C.
1,260

D.
362,880

Answer 1

the answer is
using the factoral calculator, we can find
4! x 3! x 1! = (4x3x2x1) x(3x2x1) x (1)= 24* 6 * 1 = 144
it will be placed side by side (two manners)
so it will be 2 x 144 = 288 different color patterns
the answer is A. 288

Answer 2

Answer: Option 'A' is correct.

Explanation:

Since we have given that

Total number of blocks = 8

Number of white blocks = 4

Number of yellow blocks = 3

Number of purple blocks = 1

According to question, we need to place the blocks side by side in a straight manner ,

So, Number of different colors pattern will be

`4!* 3!* 1!\\\\ =4* 3* 2* 1* 3* 2* 1* 1\\\\=144`

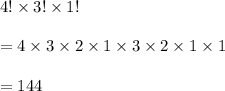
Since there are two ways to written in a straight lines so, the total number of different color patterns he could make is given by

`2* 144=288`

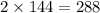
Hence, there are 288 ways to make different color patterns .

Therefore, Option 'A' is correct.