Question

In a 45°-45°-90° triangle, the length of the hypotenuse is 11. Find the length of one of the legs

Answer 1

11^2=121

121/2=60.5
sqrt 60.5=7.778 each

Answer 2

7.78 or
`(11)/(√(2) )`

Explanation:

here we are given a right angle triangle , and in a right triangle , sum of squares of sides is equal to the square of hypotenuse.

`a^2+b^2=c^2`

This is right angle scalene triangle as the two angles other than right angle are 45° each.

Hence ,

in this case we have

`a^2+a^2=c^2`

`2a^2=c^2`

`a^2=(c^2)/(2)`

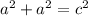
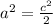
Taking square roots on both sides

`a=(c)/(√(2))`

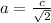
Here we have hypotenuse c given as 11

hence

`a=(11)/(√(2))`

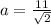
Answer