Question

The figure below is a trapezoid:10011050mZ1 =m2 =mZ3=Blank 1:Blank 2:Blank 3:

Answer 1

STEP 1: Identify and Set Up

We have a trapezoid divided by a straight line that divides it assymetrically. We know from the all too famous geometric rule that adjacent angles in a trapezoid are supplementary. Mathematically, we can express thus:

`100^o+<2+<3^{}=180^o=50^o+110^o+<1`

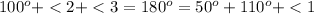
Hence, from this relation, we can find our unknown angles.

STEP 2: Execute

For <1

`\begin{gathered} 180^o=50^o+110^o+<1 \\ 180^o=160^o+<1 \\ \text{Subtracting 160}^o\text{ from both sides gives} \\ <1=180-120=60^o \end{gathered}`

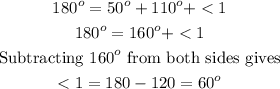
<1 = 60 degrees

For <2 & <3

We know from basic geometry that a transversal across two parallel lines gives a pair of alternate angles and as such, <1 = <3 = 60 degrees

We employ our first equation to solve for <2 as seen below:

`\begin{gathered} 100^o+<2+<3^{}=180^o \\ 100^o+<2+60^o=180^o \\ 160^o+<2=180^o \\ \text{Subtracting 160}^{o\text{ }}\text{ from both sides gives:} \\ <2=180-160=20^o \end{gathered}`

Therefore, <1 = <3 = 60 degrees and <2 = 20