Question

How to tell if second derivative is positive or negative if there are no numbers in it?

Answer 1

It's similar to how you might solve an inequality involving a polynomial. For example,


`(x+1)(x-2)>0`

First consider the case when the left side actually is zero. This happens when
`x=-1` and
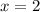
`x=2`. Pick numbers that fall to either side of these values and plug them into the inequality.

For instance, take
`x=-2` (to the left of -1),
`x=0` (between -1 and 2), and
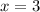
`x=3` (to the right of 2). You have


`(-2+1)(-2-2)=4>0\implies\text{ all }x<-1\text{ satisfy the inequality}`

`(0+1)(0-2)=-2<0\implies\text{ all }-1<x<2\text{ do not satisfy the inequality}`

`(3+1)(3-2)=4>0\implies\text{ all }x>2\text{ satisfy the inequality}`

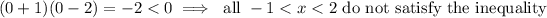
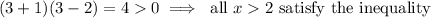
So the polynomial is positive for
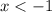
`x<-1` and
`x>2`.

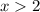
You can use a similar analysis to determine the sign of the second derivative over certain intervals.