Question

Find the dimensions of the page that will require the minimum amount of paper

Answer 1

Let's use the variable x to represent the length of the paper and y to represent the width of the paper.

If there are margins of 1 inch along the sides and 3 inches along the top and bottom, and the area with printer matter is 27 in², we can write the equation:

`(x-2)\cdot(y-6)=27`

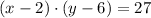
Solving for x, we have:

`\begin{gathered} x-2=(27)/(y-6) \\ x=(27)/(y-6)+2 \end{gathered}`

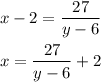
Then, the equation that we want to minimize is the area equation, so:

`\begin{gathered} A=x\cdot y \\ A=((27)/(y-6)+2)\cdot y \\ A=(\frac{27+2(y-6)_{}}{y-6})y_{} \\ A=((27+2y-12)/(y-6))y \\ A=((2y+15)/(y-6))y \\ A=(2y^2+15y)/(y-6) \end{gathered}`

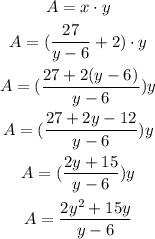
The critical points of this function are:

y = 0 (one of the roots)

y = -15/2 (one of the roots)

y = 6 (function is not defined)