Question

How do I graph r=6+3sintheta ?

Answer 1

Given:

`r=6+3\sin \theta`

Let's graph the equation.

Apply the formula:

`r=a\pm b\sin \theta`

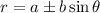
Where:

a = 6

b = 3

Thus, we have the following:

Subsitute -θ for θ to know thw axis of symmetry:

`\begin{gathered} r=6+3\sin (-\theta) \\ \end{gathered}`

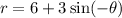
Now, solve for θ = 1 and -1:

`\begin{gathered} r=6+3\sin (1) \\ r=6.05 \\ \\ r=6+3\sin (\text{ -1)} \\ r=5.94 \end{gathered}`

Since sinθ is not equal to sin(-θ), the pole will be the point of symmetry.

To find the x-intercept, substitute 0 for θ:

`\begin{gathered} r=6+3\sin \theta \\ \\ r=6 \end{gathered}`

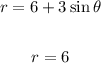
Hence, the limacon will cross the x-axis on both sides at x = 6 and -6.

Since the addition is with the sine function, the limacon will face down.

Now, input different values for θ and solve for r.

We have:

When θ = pi/2:

`r=6+3\sin ((\pi)/(2))=9`

When θ = pi:

`r=6+3\sin (\pi)=6`

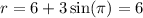
When θ = 9pi/6:

`r=6+3\sin ((9\pi)/(6))=3`

Thus, we have the points:

`((\pi)/(2),9),(\pi,6),((9\pi)/(6),3)`

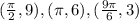
Using the coordinates we have the graph: