Question

Differentiate
y=e^[p](p+p \sqrt{p})

Answer 1

`y=e^p(p+p\sqrt p)=e^p(p+p^(3/2))`


`(\mathrm dy)/(\mathrm dp)=e^p(p+p^(3/2))+e^p\left(1+\frac32p^(1/2)\right)=e^p\left(1+\frac32p^(1/2)+p+p^(3/2)\right)`

Answer 2

`e^p(p+p√(p)+1+(3)/(2)√(p))`

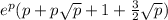
Explanation:

We are given the following information in the question:

`y = e^p(p+p√(p))\\\\y = e^p(p + p^{(3)/(2)})`

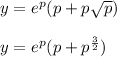
We will use the product rule to differentiate the above expression.

The product rule says that:

`\displaystyle(d(uv))/(dx) = u.(dv)/(dx) + v (du)/(dx)`

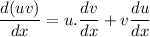
The differentiation is done in the following ways:

`\displaystyle(dy)/(dx) = (d(e^p))/(dp)(p+p√(p)) + e^p(d(p+p√(p)))/(dp)\\\\= e^p(p+p√(p)) +  e^p(1+(3)/(2)√(p))\\\\= e^p(p+p√(p)+1+(3)/(2)√(p))`

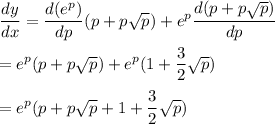
The above is the required differentiation of the given expression.