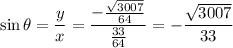Question

Let x=33/64 be the x-coordinate of the point P(x,y), where the terminal side of angle θ (in standard position) meets the unit circle. If P is in Quadrant IV, what is sin θ?

If you could, explain in steps? :))) thanks

Answer 1

Since
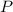
`P` lies in the fourth quadrant, you know the sine is negative.

Also since the point lies on the unit circle, the coordinates satisfy


`x^2+y^2=1\implies \left((33)/(64)\right)^2+y^2=1`

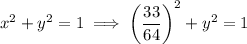
When you solve for
`y`, you have two possible solutions, which are


`y=\pm\sqrt{1-\left((33)/(64)\right)^2}=\pm\sqrt{(3007)/(4096)}=\pm(√(3007))/(64)`

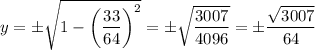
but since
`y` is negative, you take the negative root.

So,


`\sin\theta=\frac yx=(-(√(3007))/(64))/((33)/(64))=-(√(3007))/(33)`