Question

Why is cosnπ = (–1)^n true, when n could be any integer?

Answer 1

This is because when
`n` is odd, i.e.
`n=2k+1` for integers
`k`, you have


`\cos(\pm\pi)=\cos(\pm3\pi)=\cdots=\cos(\pm(2k+1)\pi)=-1`

while for even
`n`, i.e. when
`n=2k`, you have


`\cos0=\cos(\pm2\pi)=\cos(\pm4\pi)=\cdots=\cos(\pm2k\pi)=1`

Meanwhile,
`(-1)^n=-1` is
`n` is odd, while
`(-1)^n=1` if
`n` is even.

Answer 2

True

Explanation:

The value of
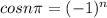`cosn{\pi}=(-1)^n` is true as:

when n is odd that is of the form
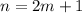`n=2m+1` where m is any integer, thus we have

`cos(\pm\pi)=cos(\pm3\pi)=...=cos(\pm(2m+1)\pi=-1`

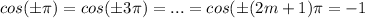
and when n is even that is of the form
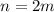`n=2m`, where m is any integer, thus we have

`cos0=cos(\pm2\pi)=....=cos(\pm2m\pi)=1`

Thus,
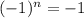`(-1)^n=-1` for when n is odd and
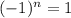`(-1)^n=1` when n is even.

Hence, the given statement is true.