Question

A man throws around a basketball from 30in above the ground. The basketball bounces off the floor and a boy catches it the distance the ball traveled from the man to the floor is 45 inches and the distance the ball traveled from the floor to the boy is 40 inches the angles formed by The basketballs path are congruent what is the distance X from the floor that the boy caught the ball? Enter your answer as a decimal round your answer to the nearest hundredth

Answer 1

The distance X from the floor that the boy caught the ball is 26.67 in.

Explanation:

Given :

A man throws around a basketball from 30 inches above the ground.

The basketball bounces off the floor and a boy catches it the distance the ball traveled from the man to the floor is 45 inches .

The distance the ball traveled from the floor to the boy is 40 inches

The angles formed by the basketballs path are congruent .

To Find : Value of x

Solution :

Since the angles formed by the basketball path are congruent so we can use trigonometric ratios.

Since angles formed by basketball path are equal i.e. ∠A = ∠D (Refer the attached file)

⇒
`Sin A = Sin D`

⇒
`Sin A= (perpendicular )/(hypotenuse) = (AB)/(AC) =(30)/(45)`

⇒
`Sin D = (perpendicular )/(hypotenuse) = (EF)/(ED) =(x)/(40)`

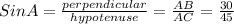
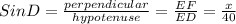
Since Sin A = Sin D

⇒
`(30)/(45) =(x)/(40)`

⇒
`(30*40)/(45) =x`

⇒
`(1200)/(45) =x`

⇒
`26.67 =x`

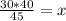
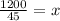
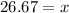
Thus , The distance X from the floor that the boy caught the ball is 26.67 in.

Answer 2

The solution for your assignment is the following:

30 / 45 = x / 40

X = 30*40 / 45

X = 26.67 inches is the distance from the floor that the boy caught the ball

Hope this helps you!