Question

There are 120.0 mL of O2 at 700. 0 mmHg and 15⁰ C. What is the number of grams present?

Answer 1

0.1498 g of O2.

Step-by-step explanation:

The Behavior of Gases => Ideal Gas Law.

The ideal gas law is a single equation that relates the pressure, volume, temperature, and the number of moles of an ideal gas, which is:

`PV=nRT,`

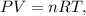
where P is pressure in atm, V is the volume in liters, n is the number of moles, R is the ideal gas constant (0.082 L*atm/mol*K), and T is the temperature in the Kelvin scale.

So we have to convert pressure from 700.0 mmHg to atm, volume from 120.0 mL to L, and 15 °C to K.

Let's convert pressure taking into account that 1 atm equals 760 mmHg, like this:

`700.0\text{ mmHg}\cdot\frac{1\text{ atm}}{760\text{ mmHg}}=0.9211\text{ atm.}`

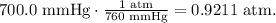
Remember that 1 L equals 1000 mL, so 120.0 mL would be equal:

`120.0\text{ mL}\cdot\frac{1\text{ L}}{1000\text{ mL}}=0.1200\text{ L.}`

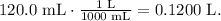
And the conversion from °C to K is just sum °C with 273, so 15 °C in K is:

`K=\degree C+273=15\degree C+273=288\text{ K.}`

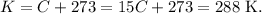
Finally, we can use the ideal gas formula, solving for 'n' (number of moles) and replacing the data that we have, as follows:

`\begin{gathered} n=(PV)/(RT), \\ \\ n=\frac{0.9211\text{ atm}\cdot0.1200\text{ L}}{0.082(L\cdot atm)/(mol\cdot K)\cdot288\text{ K}}, \\ \\ n=4.680\cdot10^(-3)\text{ moles.} \end{gathered}`

Now, the final step is to convert 4.680 x 10⁻³ moles of O2 to grams using the molar mass of O2 that can be calculated using the periodic table, which is 32 g/mol. The conversion will look like this:

`4.68\cdot10^{-3\text{ }}moles\text{ O}_2\cdot\frac{32\text{ g O}_2}{1\text{ mol O}_2}=0.1498\text{ g O}_2.`

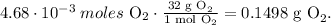
The answer would be that there are 0.1498 g of O2.