Question

in a Billiards game, peter hits a ball that is 20 in. from the wall The ball travels 34 inches until it hits the wall and bounces to a position that is 16 inches from the wall what is the distance X the ball traveled after it bounces off the wall to get to the ending position

Answer 1

27.2 Is the correct answer

Explanation:

took the test

Answer 2

27.2 inches

Explanation:

Given :

Refer the attached figure

ΔABC AND ΔEDC are right angled triangle at B and D respectively

So we will use trigonometric ratios :

`sin\theta=(perpendicular)/(hypotenuse)`

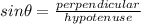
IN ΔABC perpendicular = AB=20 inches and hypotenuse = AC=34 inches

`sinC=(AB)/(AC)`

`sinC=(20)/(34)`

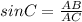
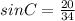
IN ΔEDC perpendicular = ED=16 inches and hypotenuse = EC=x inches

`sinC=(ED)/(EC)`

`sinC=(16)/(x)`

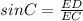
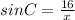
Since ∠ACB = ∠ECD

⇒
`(16)/(x)=(20)/(34)`

⇒
`(16*34)/(20)=x`

⇒
`27.2=x`

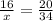
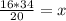
Thus distance X the ball traveled after it bounces off the wall to get to the ending position =27.2 inches