Answer:
A)
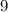
C)
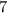
E)

F)
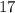
Explanation:
we know that
The Triangle Inequality Theorem, states that the sum of the lengths of any two sides of a triangle is greater than the length of the third side
Let
a,b,c ------> the length sides of the triangle
in this problem we have
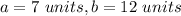
Applying the triangle inequality theorem
1)
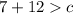
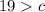 ------->
------->
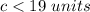 -----> inequality A
-----> inequality A
2)

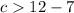 ------->
------->
 ------> inequality B
------> inequality B
The solution for the length of the third side is the interval----->
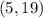
 ------> compound system of inequalities
------> compound system of inequalities
we're going to verify all the cases
If a value could be the length of the third side, then the value must be satisfy the compound system of inequalities
case A)
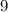
Substitute the value in the compound system of inequalities
For
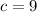
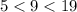 -------> is true
-------> is true
therefore
The value of
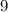 can be the length of the third side
can be the length of the third side
case B)
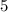
Substitute the value in the compound system of inequalities
For
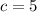
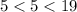 -------> is not true
-------> is not true
therefore
The value of
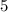 cannot be the length of the third side
cannot be the length of the third side
case C)
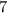
Substitute the value in the compound system of inequalities
For
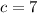
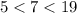 -------> is true
-------> is true
therefore
The value of
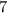 can be the length of the third side
can be the length of the third side
case D)

Substitute the value in the compound system of inequalities
For
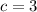
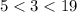 -------> is not true
-------> is not true
therefore
The value of
 cannot be the length of the third side
cannot be the length of the third side
case E)

Substitute the value in the compound system of inequalities
For

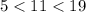 -------> is true
-------> is true
therefore
The value of
 can be the length of the third side
can be the length of the third side
case F)
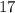
Substitute the value in the compound system of inequalities
For

 -------> is true
-------> is true
therefore
The value of
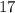 can be the length of the third side
can be the length of the third side