The function
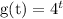 over the interval is that g(t) increases by a factor of 4
over the interval is that g(t) increases by a factor of 4
Finding the change of the function over the interval
From the question, we have the following parameters that can be used in our computation:
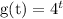
The interval is given as
From t = 3 to t = 4
The function is an exponential function
This means that it does not have a constant average rate of change
So, we have
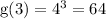
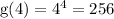
Next, we have
Change = 256/64
Evaluate
Change = 4
Hence, the change of the function over the interval is that g(t) increases by a factor of 4