Answer: The answer is 452 cubic in.
Step-by-step explanation: Given that a model of a volcano has a height of 12 in. and a diameter of 12 in.. We are to find the approximate volume of the model
Also, it is given to use that

Since a volcano is usually cone-shaped and we know that the volume of a cone with height 'h' and radius 'r' is given by

Here, r = 6 in. and h=12 in.
Therefore, the volume of the model will be
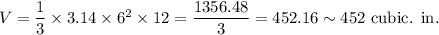
Thus, the required volume will be 452 cubic. in.