Question

How to solve question 19
thanks

Answer 1

Let
`X` be the random variable for the weight of any given can, and let
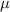
`\mu` and
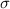
`\sigma` be the mean and standard deviation, respectively, for the distribution of
`X`.

You have


`\begin{cases}\mathbb P(X<347)=0.0015\\\mathbb P(X>377)=0.025\end{cases}`

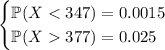
Recall that for any normal distribution, approximately 99.7% of it lies within three standard deviations of the mean, i.e.
`\mathbb P(\mu-3\sigma<X<\mu+3\sigma)=0.997`. This means 0.3% must lie outside this range,
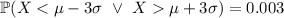
`\mathbb P(X<\mu-3\sigma~\lor~X>\mu+3\sigma)=0.003`. Because the distribution is symmetric, it follows that
`\mathbb P(X<\mu-3\sigma)=0.0015`.

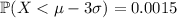
Also recall that for any normal distribution, about 95% of it falls within two standard deviations of the mean, so
`\mathbb P(\mu-2\sigma<X<\mu+2\sigma)=0.95`, which means 5% falls outside, and by symmetry,
`\mathbb P(X>\mu+2\sigma)=0.025`.

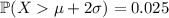
Together this means


`\begin{cases}\mu-3\sigma=347\\\mu+2\sigma=377\end{cases}`

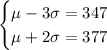
Solving for the mean and standard deviation gives
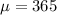
`\mu=365` and
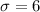
`\sigma=6`.