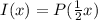Question

The function P(x) is mapped to I(x) by a dilation in the following graph. Line p of x passes through (negative 2, 4) & (2, negative 2). Line I of X passes through (negative 4, 4) & (4, negative 2).© 2018 StrongMind. Created using GeoGebra. Which answer gives the correct transformation of P(x) to get to I(x)?

Answer 1

When we're dilating a line, we can either multiply the function value by a constant

`f(x)\to kf(x)`

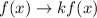
or the argument of the function

`f(x)\to f(kx)`

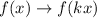
Since the y-intercept of both functions is the same, then the multiplied quantity was the argument of the function.

We want to know the constant associated to the transformation

`I(x)\to I(kx)=P(x)`

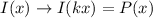
We have the following values for both functions

`\begin{gathered} I(-4)=4,\:I(4)=-2 \\ P(-2)=4,\:P(2)=-2 \end{gathered}`

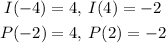
For the same y-value, we have the following correlations

`\begin{gathered} I(-4)=P(-2)=P((1)/(2)\cdot-4) \\ I(4)=P(2)=P((1)/(2)\cdot4) \\ \implies I(x)=P((1)/(2)x) \end{gathered}`

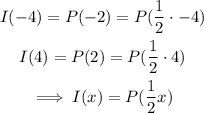
and this is our answer.

`I(x)=P((1)/(2)x)`