Question

Which of the following functions has a graph that is a line?

f(x) = x
f(x) = x 2
f(x) = |x|

Answer 1

f(x) =x

Explanation:

Given are three functions of x

We have to find the function whose graph is a straight line

We know that a straight line has constant slope throughout its domain

Let us check with this

I function

`f(x) =x`

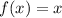
Differentiate to find the slope

Slope =1 = constant

Hence this is a straight line

2 function

`f(x) = x^ 2\\f'(x) =2x`

Thus slope depends on the value of x and not a constant. This cannot be a straight line

3 function

`f(x) =|x|\\i.e. f(x) = -x, x<0\\      f(x) = x, x\geq 0`

This function has slope 1 for positive x and -1 for negative x

Since not constant cannot be a straight line

So answer is option A

Answer 2

Right answer:

f(x)=x

In geometry, a line is straight (no curves) and has no thickness,. This extends in both directions without end, that is, infinitely. We need to find from the options the graph of a line, recall that a function
`f` from a set
`A` to a set
`B` is a relation that assigns to each element
`x` in the set
`A` exactly one element
`y` in the set
`B`. The set
`A` is the domain (also called the set of inputs) of the function and the set
`B` contains the range (also called the set of outputs).

Therefore, the right option is
`f(x)=x` as illustrated in the Figure below.