Question

Solve 6 + 5 on the sqr root of 249 - 2x = 7

Answer 1

x = 124

Step-by-step explanation

First we have to clear the term that contains x in the equation. In this case, this term is the second term. So we have tu subtract 6 from both sides of the equation:

`\begin{gathered} 6-6+\sqrt[5]{249-2x}=7-6 \\ \sqrt[5]{249-2x}=1 \end{gathered}`

Then, we have to eliminate the root. Note that in the expression inside the root there are two terms. To do this, we have to apply the "opposite" operation on both sides of the equation, which in this case is exponent 5:

`\begin{gathered} (\sqrt[5]{249-2x})^5=1^5 \\ 249-2x=1 \end{gathered}`

Now we do something similar to the first step. We want to leave on one side of the equation only the term that contains x and the rest on the other side. To do this we can either add 2x on both sides, or subtract 249 from both sides. We'll apply the first option because then we'll have a positive coefficient for x:

`\begin{gathered} 249-2x+2x=1+2x \\ 249=1+2x \end{gathered}`

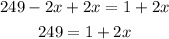
However, we now have to subtract 1 from both sides of the equation:

`\begin{gathered} 249-1=1-1+2x \\ 248=2x \end{gathered}`

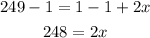
Finally, to find x, we have to divide both sides by 2:

`\begin{gathered} (248)/(2)=(2x)/(2) \\ 124=x \end{gathered}`

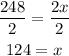
Hence, the solution to the equation is x = 124.