Question

What is the ninth term in the binomial expansion of (X-2y)^13?

Answer 1

Step-by-step explanation:

A on edge 2020

Answer 2

`329472\cdot x^5\cdot y^8`

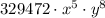
Step-by-step explanation:

Binomial expansion is:

`(a+b)^n=a^n+n\cdot a^(n-1){\cdot b}+(n(n-1))/(2)\cdot a^(n-2)\cdot b^2+------+b^n`

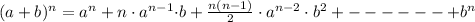
Here in given expression we have a=x , b=-2y and n = 13

general formula for binomial expansion is:

`T_(r+1) =^nC_r\cdot a^(n-r)\cdot b^r`

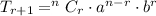
Since,
`T_(r+1)`

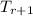
r should be one number less than the term we need to find so it will become the number we need to find like here we have to find 9th term so, r=8

substituting the values in the genral formula we will get

`^13C_8\cdot x^(13-8)\cdot (-2y)^8`

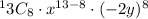
After substituting the values we will get

`(13!)/(8!\cdot 5!)\cdot x^5\cdot (-2y)^8}`

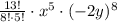
After simplification we will get

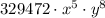`329472\cdot x^5\cdot y^8` which will be the 9th term of the expansion