Question

What is a feature of function g if g(x) = log (x-4) -8

Answer 1

Hope this helps ;)

Explanation:

Answer 2

The domain and range of the logarithmic function are

`\begin{gathered} \text{domain}(\log x)=(0,\infty) \\ \text{range}(\log x)=(-\infty,\infty) \end{gathered}`

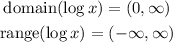
Therefore, if

`g(x)=\log (x-4)-8`

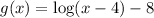
We require that

`\begin{gathered} x-4>0 \\ \Rightarrow x>4 \end{gathered}`

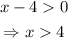
Notice that the -8 term does not affect the range of function g(x); thus,

`\begin{gathered} \text{domain}(g(x))=(4,\infty) \\ \text{range}(g(x))=(-\infty,\infty) \end{gathered}`

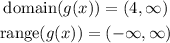
Set g(x)=-8; then,

`\begin{gathered} \Rightarrow\log (x-4)-8=-8 \\ \Rightarrow\log (x-4)=0 \\ \Rightarrow x=5 \end{gathered}`

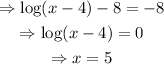
Therefore, y=-8 is not an asymptote of g(x), and, as shown above, the domain and range of g(x) are x>4, y->all real numbers.

Calculate the limit when x->4 as shown below,

`\lim _(x\to4)g(x)=(\lim _(x\to4)\log (x-4))-8=(-\infty)-8=-\infty`

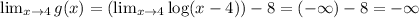
Therefore, there is a vertical asymptote at x=4