The domain and range of the logarithmic function are
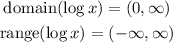
Therefore, if
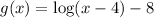
We require that
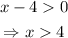
Notice that the -8 term does not affect the range of function g(x); thus,
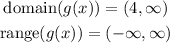
Set g(x)=-8; then,
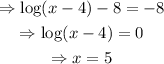
Therefore, y=-8 is not an asymptote of g(x), and, as shown above, the domain and range of g(x) are x>4, y->all real numbers.
Calculate the limit when x->4 as shown below,
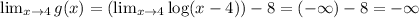
Therefore, there is a vertical asymptote at x=4