Answer:
Option B is correct
factor completely of
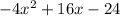 is
is

Explanation:
GCF(Greatest Common Factor) states that the largest factor that divides the polynomial.
Given the expression:
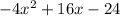
By definition of GCF we have;
Factor a GCF of the given expression.
Since GCF of
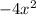 ,
,
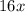 and -24 is -4
and -24 is -4
then;

Therefore, factor completely of
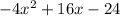 is
is
