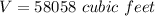Question

A mound of gravel is shaped like a cone. Circumference at the bottom is 250 feet. The Pile is 35 feet high. how many cubic feet of gravel are in the pile. Round 2 decimal places in each step and round the final answer to the nearest cubic foot

Answer 1

Volume of a cone = (1/3) π r² h = (1/3) (Area) (h) Where r = radius of the circular base of the cone , h = height The volume is in units cubed.
To find the area (π r²) of the circular base from it's circumference: Divide the circumference by 2π: 250/2π = 39.7887 <-----That is the radius.
Now find the area of the circular base: πr²: π (39.7887)² = 4973.59
Now find the volume of the cone: (1/3) π r² h: (1/3) (4973.59) (35) = about 58,025.24 ft. cubed

Answer 2

The answer is: 58058 cubic feet.

Explanation:

It is given that:

A mound of gravel is shaped like a cone. Circumference at the bottom is 250 feet.

This means that the circumference of the circle is: 250 feet

i.e. if r is the radius of the bottom of the cone then

`2\pi r=250\\\\i.e.\\\\r=(250)/(2\pi)\\\\i.e.\\\\r=(125)/(\pi)\\\\i.e.\\\\r=39.8089\ feet`

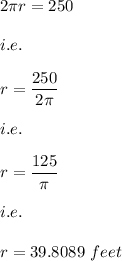
Now, on rounding to 2 decimal places we have:

`r=39.81\ feet`

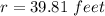
Also, the height(h) of the cone is given as:

`h=35\ feet`

The volume(V) of cone is given by:

`V=(1)/(3)* \pi* r^2* h\\\\i.e.\\\\V=(1)/(3)* 3.14* (39.81)^2* 35\\\\i.e.\\\\V=58057.82913\ cubic\ feet`

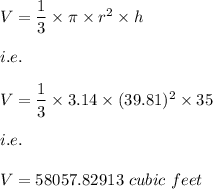
which to the nearest foot is given by:

`V=58058\ cubic\ feet`