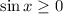
for all
![x\in[0,\pi]](https://img.qammunity.org/2018/formulas/mathematics/college/e92w2z77ctdzrj69wmoxxwtr7knkneq8i9.png)
, while
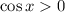
for
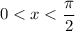
and
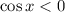
for
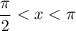
. So you already know that
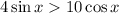
over the second half of the interval.
In the first half,

is an increasing function, from
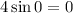
to
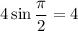
. Meanwhile
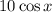
is a decreasing function, from

to
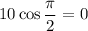
. Therefore there must be a point between 0 and
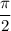
where the two curves intersect. So we find it:
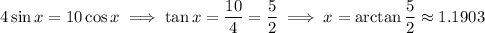
So we know that
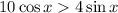
in

, and
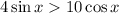
in
![\left(\arctan\frac52,\pi\right]](https://img.qammunity.org/2018/formulas/mathematics/college/ac6mbanquwnr0f9bkjalm729g0bu4chxmo.png)
.
The area between the curves is then
