Question

Victoria and her children went into a grocery store and she bought $9 worth of applesand bananas. Each apple costs $1.50 and each banana costs $0.50. She bought a totalof 8 apples and bananas altogether. Determine the number of apples, x, and thenumber of bananas, y, that Victoria bought.Victoria boughtapples andbananas.

Answer 1

We will determine the solution as follows:

*First: From the text, we have the following expressions:

`x+y=8`

&

`1.50x+0.5y=9`

Here x represents apples and y represents bananas.

*Second: From the first expression, we solve for either x or y, that is [I will solve for ]:

`x+y=8\Rightarrow x=8-y`

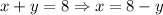
*Third: Now, using the value for x, we replace in the second expression and solve for y, that is:

`1.50x+0.5y=9\Rightarrow1.50(8-y)+0.5y=9`
`\Rightarrow12-1.50y+0.5y=9\Rightarrow-y=-3`
`\Rightarrow y=3`

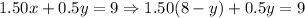
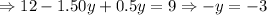
*Fourth: We replace the found value of y on the first expression and solve for x:

`x+y=8\Rightarrow x+3=8`
`\Rightarrow x=5`

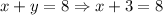
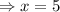
So, the number of apples was 5 and the number of bananas was 3.