A cylinder and a cone have the same volume. The cylinder has radius x and height y. The cone has radius 2x. Find the height of the cone in terms of y.

Question

asked Jul 3, 2018 171k views

1 Answer

Richard Chambers · Answer 1 · 2018-07-07T02:29:02+0000

Answer:

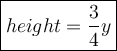
$\large\boxed{height=(3)/(4)y}$

Explanation:

The formulas of a volume of

a cylinder:

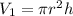
$V_1=\pi r^2h$

a cone:

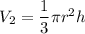
$V_2=(1)/(3)\pi r^2h$

r - radius

h - height

Substitute

The cylinder:

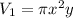
$V_1=\pi x^2y$

The cone:

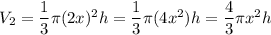
$V_2=(1)/(3)\pi (2x)^2h=(1)/(3)\pi(4x^2)h=(4)/(3)\pi x^2h$

The cylinder and the cone have the same volume. Therefore we have the equation:

$(4)/(3)\pi x^2h=\pi x^2y$ divide both sides by πx²

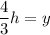(4)/(3)h=y multiply both sides by 3/4

$(3\!\!\!\!\diagup^1)/(4\!\!\!\!\diagup_1)\cdot(4\!\!\!\!\diagup^1)/(3\!\!\!\!\diagup_1)h=(3)/(4)y\\\\h=(3)/(4)y$