Question

graph a line that is perpendicular to the given line. determine the slope of the given line and the one you graphed in simplest form. click and drag on the graph to draw a line. click and drag to plot a perpendicular line. the line will change colors when a parallel or perpendicular line is drawn accurately.

Answer 1

The line given passes through two points. These are (-6,0) and (0,-8).

Remember that two lines are perpendicular if the product of their slopes is -1. So, the first thing we're going to do is to find the slope of the line given.

The slope between two points (x1,y1) and (x2,y2) can be found using the formula:

`m=(y_2-y_1)/(x_2-x_1)`

If we replace our values:

`m=(-8-0)/(0-(-6))=(-8)/(6)=-(4)/(3)`

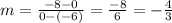
To find other perpendicular line to this one, we have to find a number which multiplication with -4/3 is -1.

This number is clearly 3/4. Because

`\begin{gathered} m_1\cdot m_2=-1 \\ -(4)/(3)\cdot m_2=-1 \\ \\ m_2=(3)/(4) \\ \\ -(4)/(3)\cdot(3)/(4)=-1 \end{gathered}`

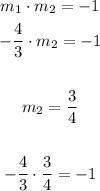
Therefore, the slope of the perpendicular line must be 3/4, and the original slope is -4/3.

If we graph this: