Question

Shaun deposits $3,000 into an account that has an rate of 2.9% compounded continuously. How much is in the account after 2 years and 9 months?

Answer 1

The formula for finding amount in an investment that involves compound interest is

`A=Pe^(it)`

Where

A is the future value

P is the present value

i is the interest rate

t is the time in years

e is a constant for natural value

From the question, it can be found that

`\begin{gathered} P=\text{ \$3000} \\ i=2(9)/(12)years=2(3)/(4)years=2.75years \end{gathered}`
`\begin{gathered} e=2.7183 \\ i=2.9\text{ \%=}(2.9)/(100)=0.029 \end{gathered}`

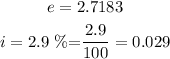
Let us substitute all the given into the formula as below

`A=3000* e^(0.29*2.75)`
`\begin{gathered} A=3000*2.21999586 \\ A=6659.987581 \end{gathered}`

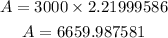
Hence, the amount in the account after 2 years and 9 months is $6659.99