The formula for finding amount in an investment that involves compound interest is
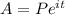
Where
A is the future value
P is the present value
i is the interest rate
t is the time in years
e is a constant for natural value
From the question, it can be found that
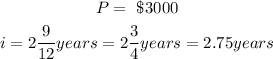
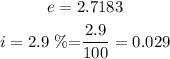
Let us substitute all the given into the formula as below

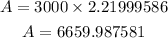
Hence, the amount in the account after 2 years and 9 months is $6659.99