Answer:
The radius of the planter, rounded to the nearest inch is, 4 inches
Explanation:
As per the statement:
A gardener purchases a ceramic planter, in the shape of a hemisphere, for a small batch of leftover annuals
The volume of a hemisphere is modeled by the function as:
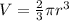 ....[1]
....[1]
where,
V is the volume and r is the radius of the hemisphere.
To write a model for the radius as a function of the volume.
Divide equation [1] to both sides by
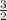 we have;
we have;
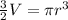
Divide both sides by
 we have;
we have;

or
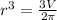
⇒
![r = \sqrt[3]{(3V)/(2 \pi)}](https://img.qammunity.org/2018/formulas/mathematics/college/vubp4ripo189ag12evivb7k0cry4awkwb3.png) ....[2]
....[2]
It is also given that:
The label on the planter says that it holds approximately 134 cubic inches of potting soil.
⇒
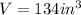 and use 3.14 for pi.
and use 3.14 for pi.
Substitute these in [2] we have;
![r = \sqrt[3]{(3 \cdot 134)/(2 \cdot 3.14)}](https://img.qammunity.org/2018/formulas/mathematics/college/851ipd2g0wtn3h4nnrp26ytrt3emd4c003.png)
⇒
![r = \sqrt[3]{(402)/(6.28)}= \sqrt[3]{64.0127389}](https://img.qammunity.org/2018/formulas/mathematics/college/cee0udd20fg3mozl9bwltg5ljwq4nsu3si.png)
Simplify:
r = 4.00026538 inches
Therefore, the radius of the planter, rounded to the nearest inch is, 4 inches