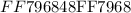We have a one-dimensional horizontal line segment. Three points are indicated on the line as follows:
In the above sketch we have first denoted a reference point at the extreme left hand as ( Ref = 0 ). This is classified as the origin. The point ( A ) is located on the same line and is at a distance of ( 21 units ) from Reference ( Ref ). The point ( B ) is located on the same line and is at a distance of ( 66 units ) from Reference ( Ref ).
The point is located on the line segment ( AB ) in such a way that it given as ratio of length of line segment ( AB ). The ratio of point ( P ) from point ( A ) and from ( P ) to ( B ) is given as:
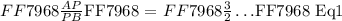
The length of line segment ( AB ) can be calculated as follows:
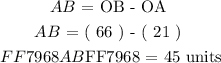
We can form a relation for the line segment ( AB ) in terms of segments related to point ( P ) as follows:
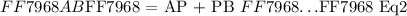
We were given a ratio of line segments as ( Eq1 ) and we developed an equation relating the entire line segment ( AB ) in terms two smaller line segments as ( Eq2 ).
We have two equation that we can solve simultaneously:
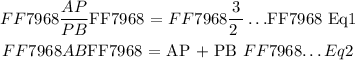
Step 1: Use Eq1 and express AP in terms of PB.
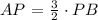
Step 2: Substitute ( AP ) in terms of ( PB ) into Eq2
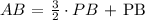
We already determined the length of the line segment ( AB ). Substitute the value in the above expression and solve for ( PB ).
Step 3: Solve for PB
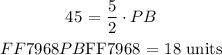
Step 4: Solve for AP
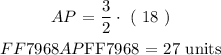
Step 5: Locate the point ( P )
All the points on the line segment are located with respect to the Reference of origin ( Ref = 0 ). We will also express the position of point ( P ).
Taking a look at point ( P ) in the diagram given initially we can augment two line segments ( OA and AP ) as follows:
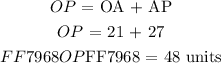
The point ( P ) is located at.
Answer: